Читать Векторные свойства гравитационного потенциала - Петр Путенихин

На данной странице вы можете читать онлайн книгу "Векторные свойства гравитационного потенциала" автора Петр Путенихин. Общий объем текста составляет эквивалент 10 бумажных страниц. Произведение многоплановое и затрагивает разнообразные темы, однако его жанры наиболее вероятно можно определить как физика, математика, астрономия. Книга была добавлена в библиотеку 09.08.2023, и с этой даты любой желающий может удобно читать ее без регистрации. Наша читалка адаптирована под разные размеры экранов, поэтому текст будет одинаково хорошо смотреться и на маленьком дисплее телефона, и на огромном телевизоре.
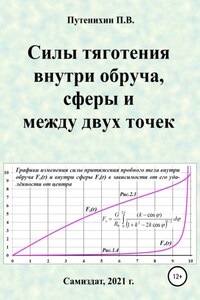
Приведено доказательство векторной природы гравитационного потенциала, согласно которой гравитационный потенциал в любой точке бесконечной Вселенной равен нулю. Напротив, согласно скалярным представлениям о гравитационном потенциале, в стационарной Вселенной гравитационный потенциал равен бесконечности, причём в любой точке пространства. Однако этот потенциал входит в уравнение всемирного тяготения, имеющего явно векторный характер. Закон неявно содержит в себе не только ускорение свободного падения, векторную величину, но и формирующий его гравитационный потенциал, который автоматически получает статус вектора.